首先,什么是线性变换?
简化了一万倍来说,线性变换主要是在描述符合这两种性质的变换:一是要可加,二是要能数乘。
也就是说,对于空间中所有向量 v1,v2 ,以及任意数量 k1,k2 ,如果有:
A(k1v1+k2v2)=k1A(v1)+k2A(v2)
符合这种规律的 A 就叫线性变换。而一次矩阵乘法正好可以代表一次线性变换。
为什么叫“线性”变换呢?感性地来说,因为它很“线”。
我们可以直观地从下面这张图看出原因:
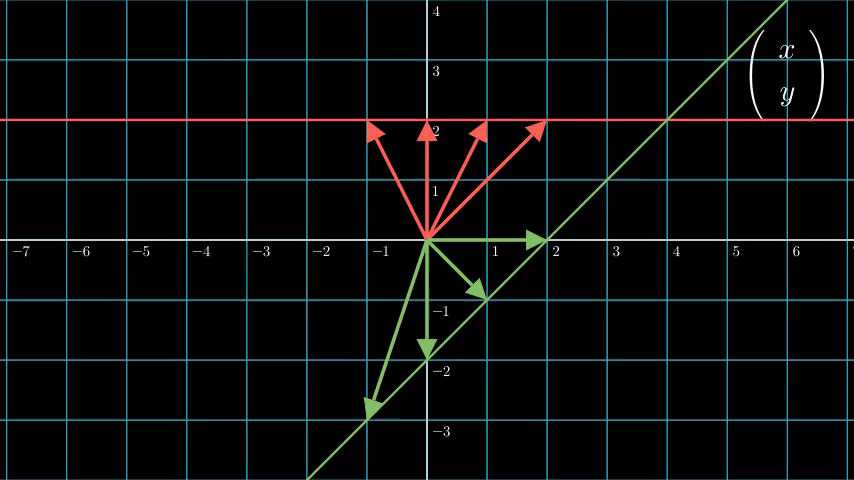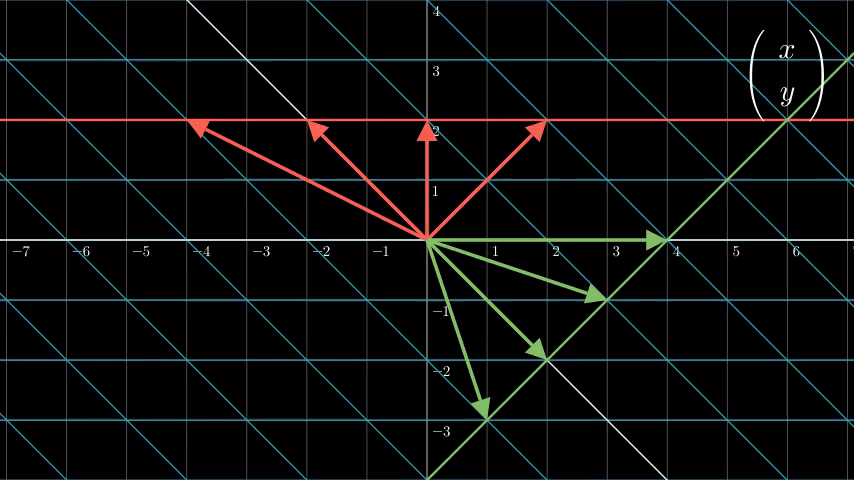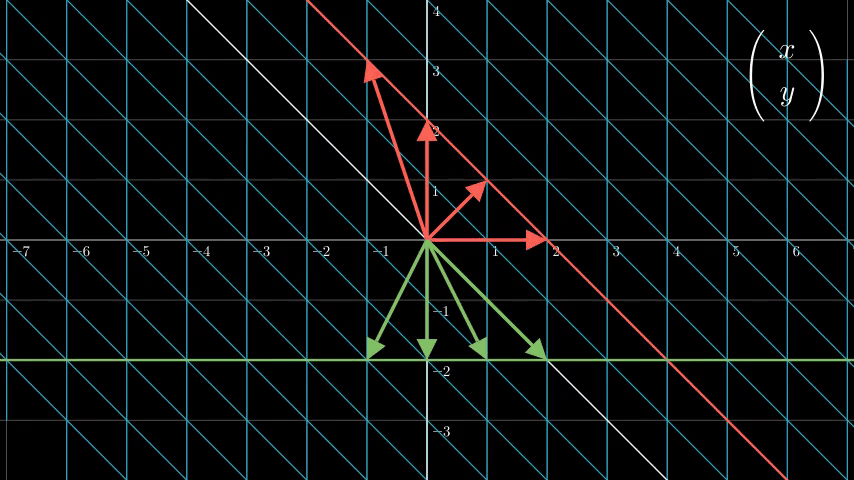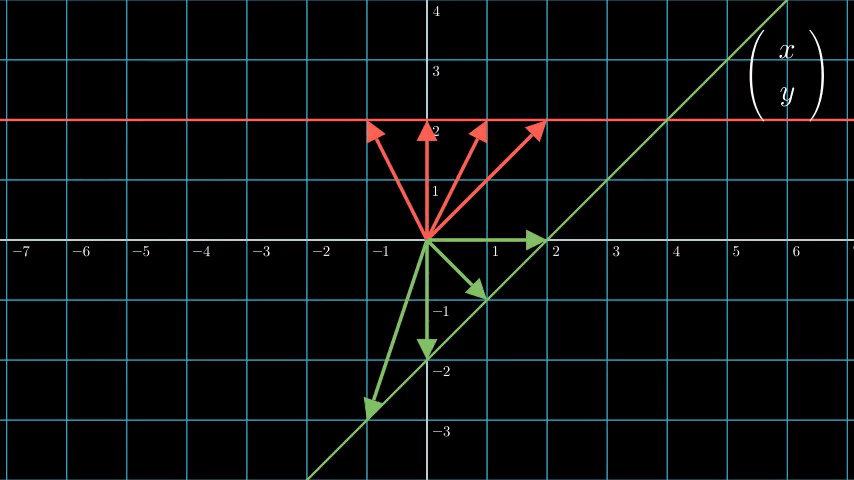
我们可以看到,在同一直线上的点,经过同一线性变换后还在同一直线上。所以它很“线”。
另一方面,我们可以找一找最简单的线性变换:
考虑函数:
f(x)=k0x
我们都知道这是一条过原点的直线。
而从另一方面想,其实这个函数对于任意一维向量(实数) x1,x2 , 与任意数量(实数) k1,k2 , 都有:
f(k1x1+k2x2)=k1k0x1+k2k0x2=k1f(x1)+k2f(x2)
即, xy 平面上过原点的直线(正比例函数)本身就是一种从 x 轴到 y 轴的线性变换。
关于线性变换, 3blue1Brown 上有更详细更感性的介绍,大家感兴趣可以前往观看。
为什么普通的线性变换不能表示点平移?
从上面的感性介绍来看,我们知道线性变换的性质就是可加和数乘,写成等式就是:
A(k1v1+k2v2)=k1A(v1)+k2A(v2)
而当两个向量都为零向量时,等式就会简化成:
A(0)=A(0)+A(0)
解一下方程,就可以知道,对任意线性变换 A,都会有:
A(0)=0
也就是说,不管是哪个线性变换 A ,原点经过变换后都必须只能是在原点不变。如果变换后原点的位置变了,那它就一定不是线性变换。
我们从下图也可以看出,对于切变 (1011) 、伸缩 (20021)、旋转 (2321−2123) 这些经典的线性变换,变换后原点都不会变。
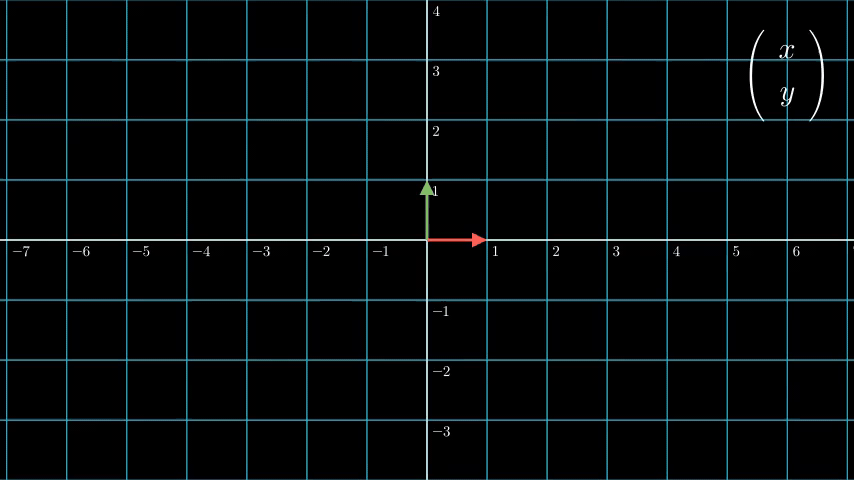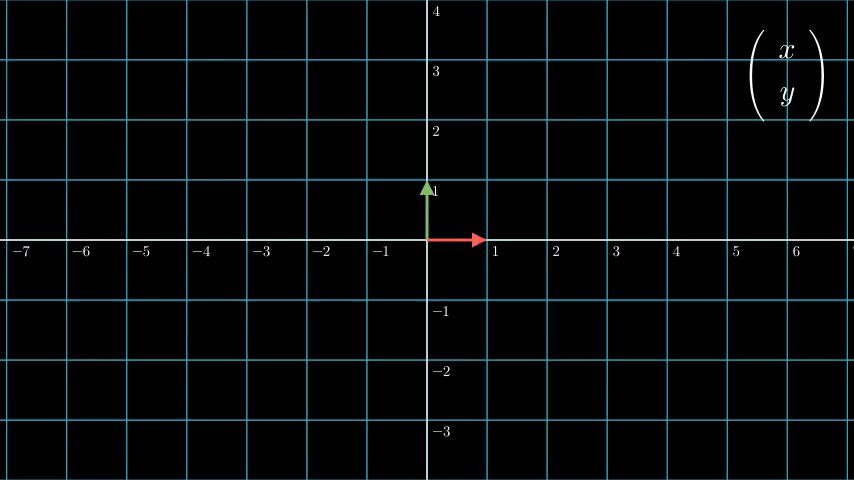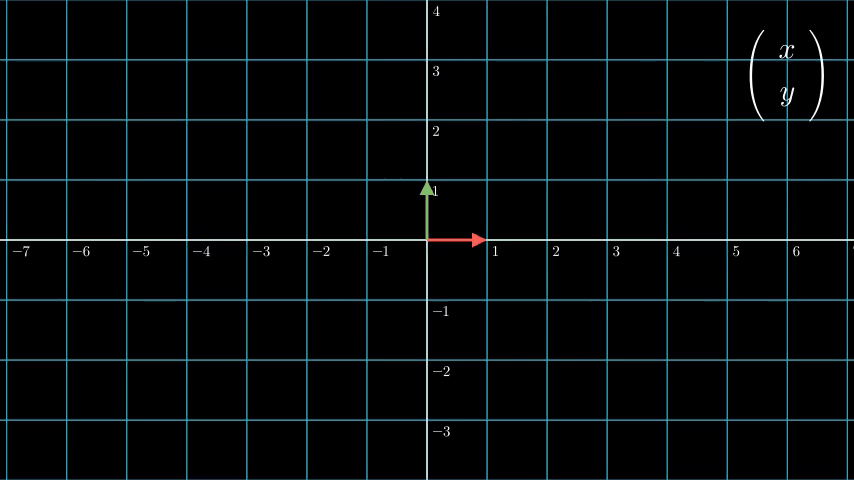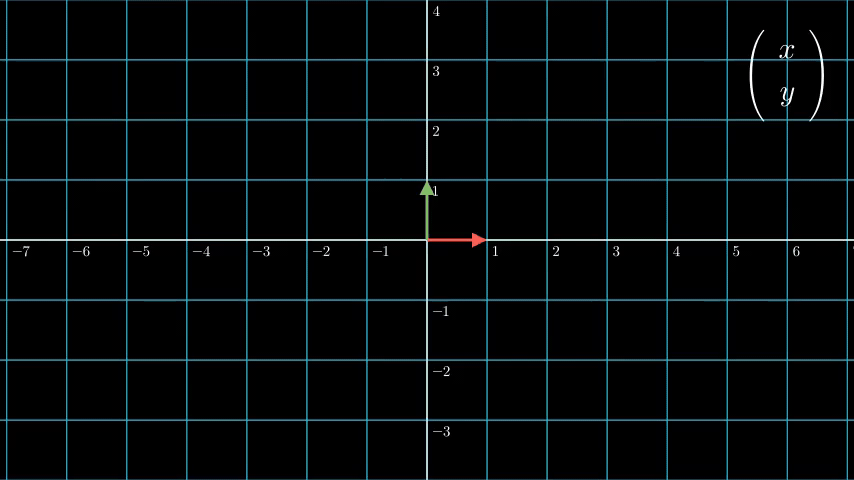
但是平移这种变换不一样。原点经过平移后,是一定不会还留在原点的。因此平移不是一种线性变换,自然也不能用矩阵来表示。
为什么基于齐次坐标下的线性变换就可以表示平移?
我们先来看一下齐次坐标做了些什么。
在上面传统的线性变换中,我们不会考虑向量与点的区别。一个二维坐标 (x,y) 既能代表那个坐标上的点,也能代表从原点到 (x,y) 的向量。这时,点与向量是一一对应的。
但如果要考虑平移,点与向量就不能再一一对应了,因为对向量平移没有意义(不考虑物理中力矩的场景)。
所以在齐次坐标下,我们需要区分这个坐标代表的是点还是向量。
以二维空间为例,齐次坐标就是在二维空间上加了第三个维度 w 轴,二维空间里的点在 w 轴上的值为 1 ,而二维向量在 w 轴上的值对应为 0 :
Pv=(xy1)=(vxvy0)
从字面上看可能还是不太明显,让我们试着把二维空间齐次坐标强行转化为三维空间坐标看看:
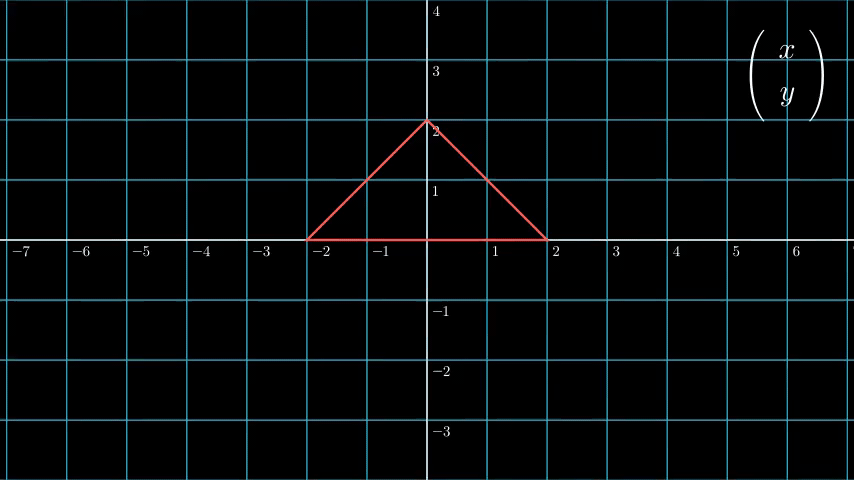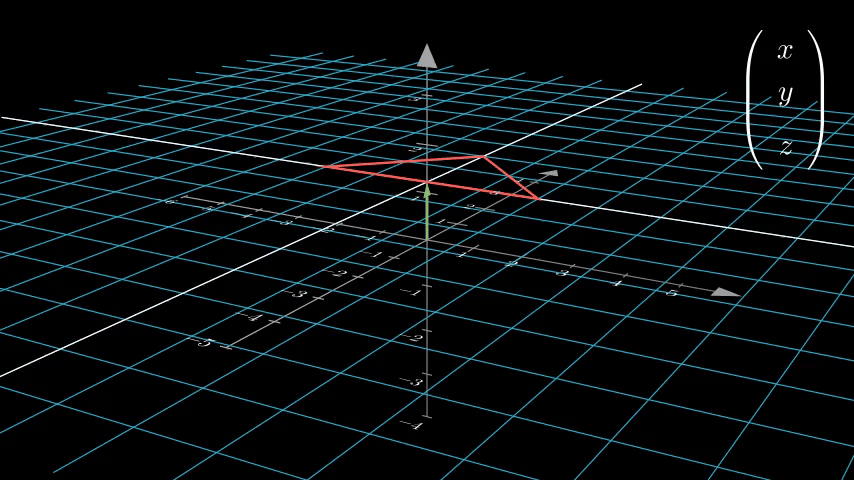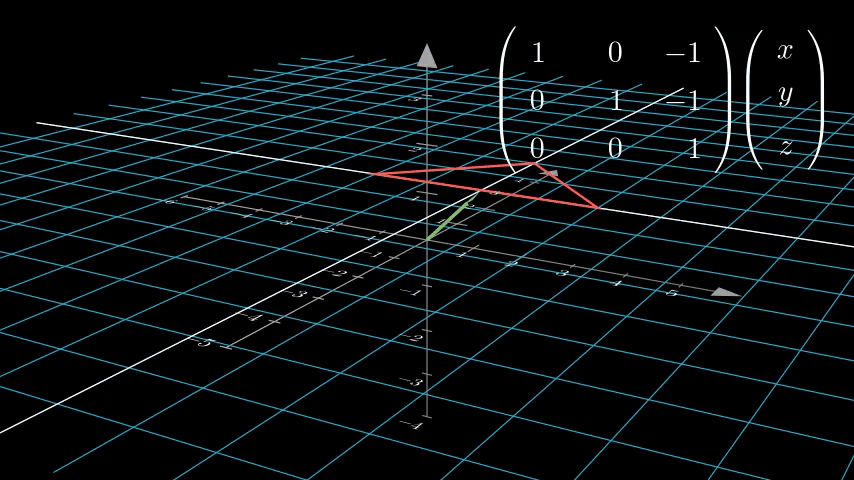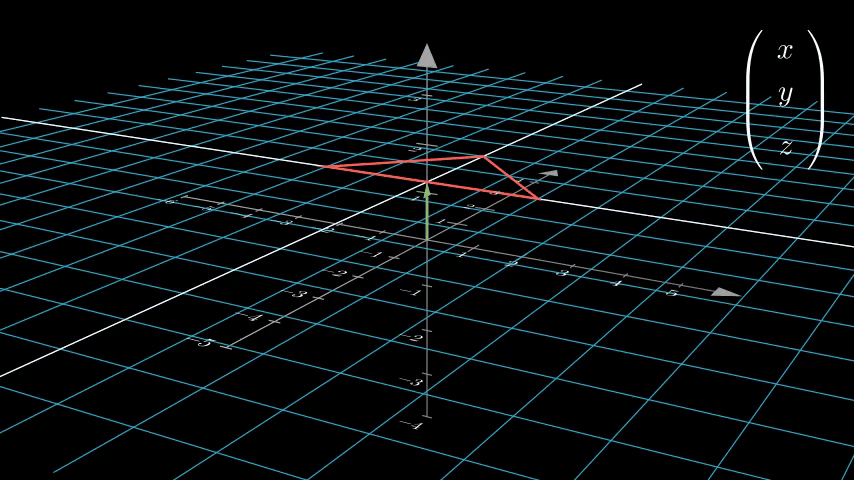
我们发现,原来二维空间中的点,被投射到三维空间中 w = 1 的平面上了!
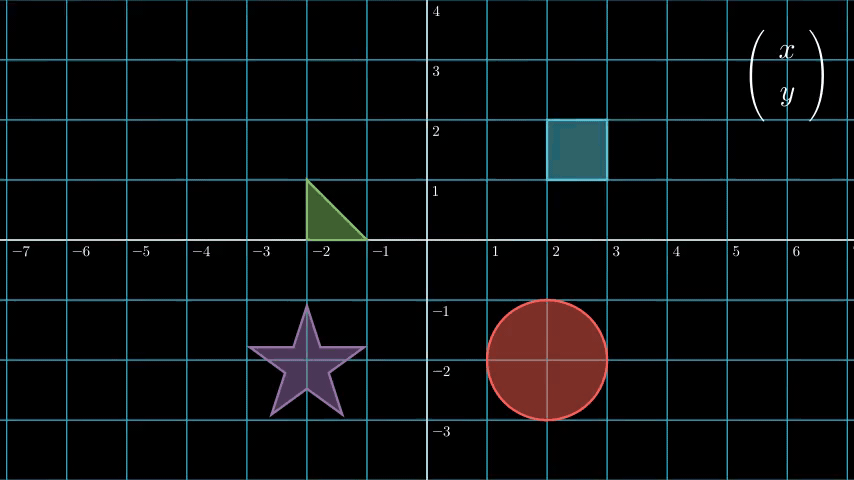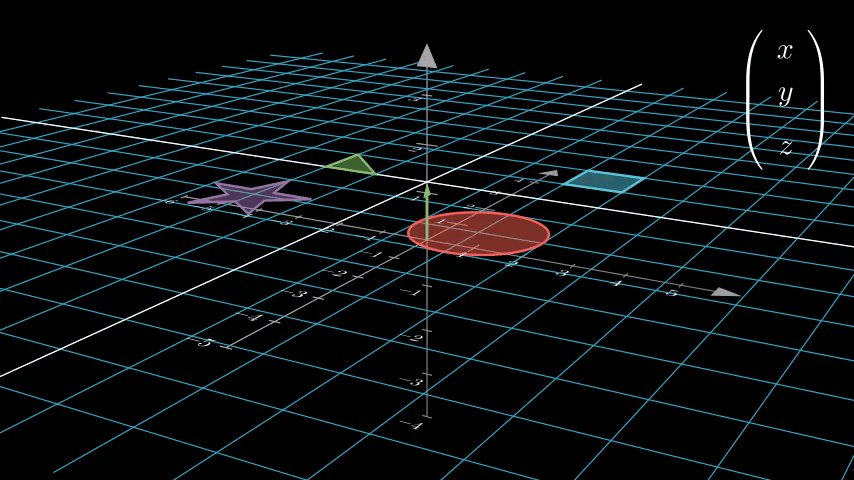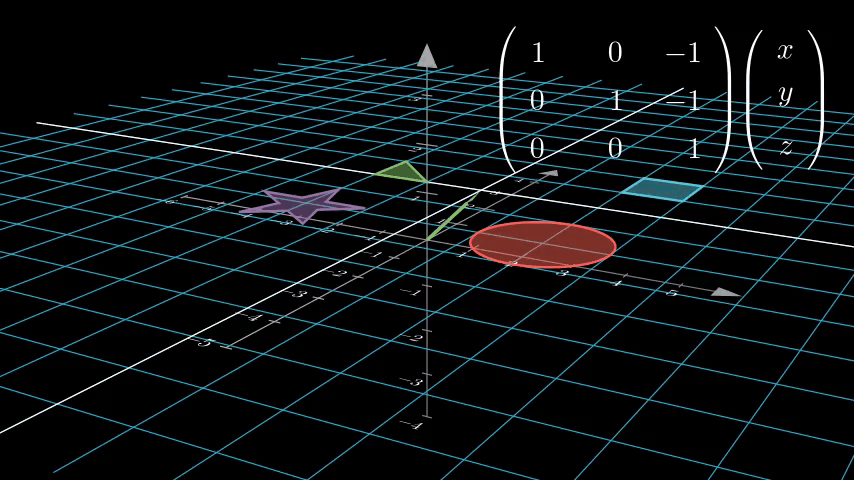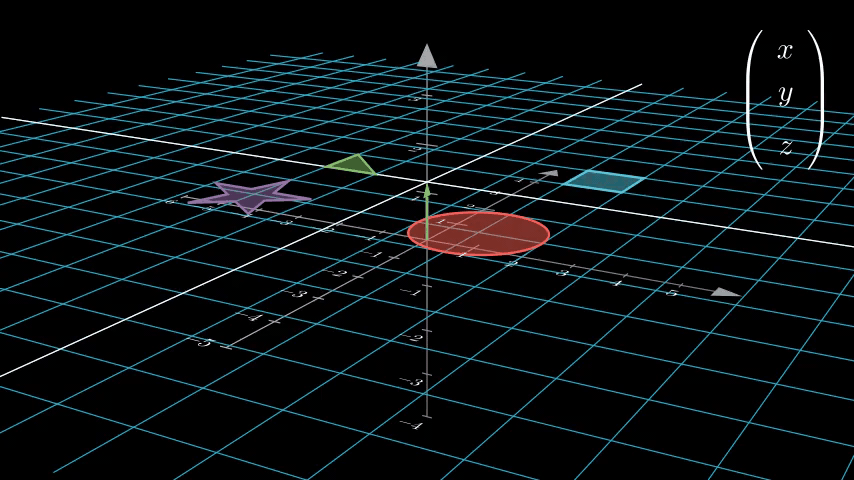
这样一来,二维空间齐次坐标下的平移矩阵也很好理解了:
将平面沿向量(x,y)平移:100010xy1
这不就是三维空间中在 w 轴上做切变时的变换矩阵嘛!
我们可以重点关注一下 001 这个向量。
从齐次坐标的定义来看,这个向量对应着二维空间中的原点 POrigin=(00) 。而由矩阵乘法计算可知,经过 A=100010xy1 对应的线性变换后, 001 这个向量会被映射到 xy1 上。也就是说,二维空间原点 POrigin=(00) 经过变换后会变为 POrigin′=A(POrigin)=(xy) 。
而对于二维空间中的向量 v=(vxvy) ,其齐次坐标下 w 轴方向分量为 0 ,因此 w 轴方向上的切变并不会影响二维空间中的向量。即 v′=A(v)=v 。
而对于原来二维空间中的其他点的坐标:
P=(x0y0)
其实可以理解为原点坐标再加上一个偏移向量:
P=(00)+(x0y0)=POrigin+vx,y
而在齐次坐标下,点坐标 = 原点坐标 + 偏移向量 这一等式仍然成立:
P=x0y01=001+x0y00=POrigin+vx,y
而由于切变是线性变换,因此有:
P′=A(P)=A(POrigin+vx,y)=A(POrigin)+A(vx,y)=POrigin′+vx,y
因为切变前后偏移向量没有发生变化,因此二维空间上的点经变换后相对于原点的方向、距离都没有发生变化。由此也可得出,原先由二维空间中的点组成的图案,经齐次坐标下 w 轴的切变后,其大小、形状、方向都不会发生变化。
而这种大小、形状、方向都不变化,只有整体位置发生了变化的变换,正是我们一般所说的“平移”。因此在齐次坐标下,我们能通过线性变换(aka 矩阵乘法)表示平移。
其实 100010xy1 对应切变作用后各点坐标如何变化这个过程, 3Blue1Brown 的这个视频 有更直观明了的解释,大家可以参考。
总结一下
Q: 为什么普通的矩阵乘法不能表示平移?
A: 因为矩阵乘法只能表示线性变换。平移不是线性变换。
Q: 为什么在齐次坐标下的矩阵乘法又能表示平移?
A: 因为齐次坐标增加了一个维度。平移变换矩阵其实是在新增的这个维度上做切变(一种线性变换)。切变后的结果正好就是原坐标中的平移变换。



