Ryo's Blog
Articles
Ideas
Tags
Clips

如何手撕一个堆

数据结构
算法
算法竞赛

如何手撕一个堆

写在前面

在参加如AtCoder等算法竞技，或是刷Leetcode等算法题时，我们总是不可避免地遇到堆这种数据结构。

当然，一般来说我们只要理解堆，知道堆的性质，知道怎么样用堆就足够了。在做题时只需要调用系统类库即可——在参加AtCoder时你甚至不会有时间去自己实现一个堆。

但是，如果哪一天你把编程语言的类库全忘光了，又遇到一题需要频繁求最值的题目——你明知这里要用堆，却又忘记该调用的类名了，咋办？我还真遇到过这问题：三年没刷算法，只能对着一道自己明显会的题干着急，愣是想不起PriorityQueue的名字。这时候，只能自己实现一个堆出来了。

首先要理解，然后才能实现

就像人总不会忘记自行车怎么骑一样，只要理解了数据结构的原理，身体就会自动来帮我们记忆，总不会忘。那要怎么理解一个堆呢？

先抓住重点：堆是一种树结构

首先最重要的，要理解堆是一种树结构。不管实际是基于数组实现还是别的什么实现，逻辑结构是树结构没变的。

再进一步，在堆这种树结构中，最重要的约束就是：对于树中的每个节点，总有父节点大于两个子节点（以大顶堆为例，下同）。

如此一来，大小关系在树中层层传递，最终可得树的根节点（堆顶）就是整个堆的最大节点，读取堆中最大值的时间复杂度为O(1)。而我们使用堆也一般是为了利用这种堆顶元素就是最大值的特点，读取、删除操作一般会限制为只允许读取、删除堆顶元素。

而且我们可以注意到，与二叉查找树比起来，堆的约束十分之弱：堆只约束父节点与子节点的大小关系，而不需要管左右子树的大小关系，甚至不需要管左右两个子节点之间谁大谁小。这样一来堆就有很多很好的性质了：

  1. 堆并不关注左右子树之间的大小情况，那么要维护一个堆，基本只需要做交换父节点与子节点的操作，而不需要像二叉查找树那样做各种旋转操作。
  2. 因为维护一个堆不需要做旋转操作，那么几乎不需要花任何代价，就可以把堆的树结构维持在完全二叉树状态。因此堆的物理结构可以设计得很紧凑，可以使用数组进行实现。
  3. 因为堆可以维持在完全二叉树状态，那么堆的树结构的高度就可以控制为O(logn)范围内。而如上所述，要维护一个堆我们不需要关注左右子树的关系。因此我们要在堆上做增删操作，都只需要上下交换若干次父子节点。而交换次数最多时，也只是从树根一直交换到树叶，或是从树叶一直交换到树根，最多交换logn次。那么我们可得：堆的增删操作最坏时间复杂度为O(logn)。

再抓基本操作：上浮与下沉

上面也提到，要维护一个堆，我们只需要上下交换若干次父子节点即可。若一个节点过大，就跟他的父节点向上交换；若一个节点过小，就跟他的子节点向下交换。

假设p节点过大破坏了堆结构，即p节点比其父节点g还要大，向上交换如下图：

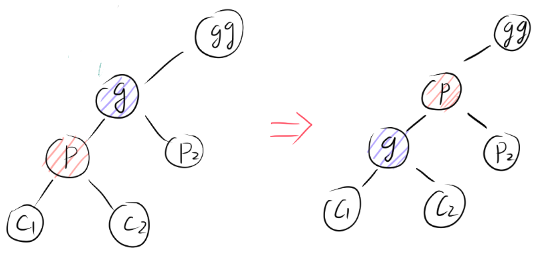
p与g交换

由于除了p过大破坏堆结构以外，其他节点都符合堆结构，则有：

  1. p > g > p2
  2. g > 原p > c1与c2

则向上交换后有只有一种破坏堆结构的可能性：p节点过大，比gg节点还要大。而解决方法也很简单，就是递归地进行向上交换，最坏情况下一直交换到堆根节点为止。

同理可得，p节点过小，小于他的子节点时，向下交换后有可能需要递归地向下交换，最坏情况下一直交换到叶子节点为止。要注意向下交换时需要先比较一下两个子节点的大小，再跟较大的子节点交换，才能交换后的大小关系符合堆的要求。

为了简化，我们把前面那种递归地向上交换称为上浮操作，把后面这种递归地向下交换称为下沉操作。所有需要维护堆结构的操作：增、删、建堆，都可以拆分为上浮操作或是下沉操作的组合。

各种接口的逻辑

插入元素——入堆

把一个元素p加入堆中，我们可以先把p加到堆尾，然后对p做上浮操作。

虽然堆是一个树结构，但由于堆可以用数组实现，那我们只要用O(1)的时间就可以找到堆尾。而如上面所述上浮操作最多交换到根节点 。由于用数组实现的堆是完全二叉树，交换到根节点时间复杂度为O(logn)。因此我们可得入堆的最坏时间复杂度为O(logn)。

删除堆顶元素——出堆

我们从堆中删除元素时，一般只会删除堆顶元素。

删除堆顶元素时，我们可以摘出堆尾元素p填到堆顶的空缺中，再对p做下沉操作。找到堆尾元素需要O(1)时间，下沉操作最多交换到叶子节点，时间复杂度为O(logn)。因此出堆最坏时间复杂度为O(logn)。

这里加点餐：出堆时把堆尾元素p放到堆顶后下沉，而p原先在堆中的最下层，一般在整个堆中都算较小的元素。因此下沉p时有较大概率需要一直把p下沉到最下层或是倒数第二层，即出堆时最坏情况出现概率较高。

堆的初始化——建堆

建立一个堆，我们有两种思路：

  1. 将元素一个一个插入，即对每个元素都做一次入堆操作。
  2. 当节点p左子树和右子树都各自为一个堆时，只要把p下沉就可以把左右两个堆合并成一个更大的堆。即不断地进行堆合并操作。

下面我们来分析这两种建堆策略。

元素逐个入堆

上面说到，入堆就是把元素加到堆尾，再做上浮操作。把元素逐个入堆，就是把元素逐个上浮。

插入第i个元素时，堆的大小为ii（在不影响计算情况下的近似，下同），则有堆的高度为，则上浮时间复杂度为：

T(i)=logiT(i) = logi

那么把所有元素上浮，则总时间复杂度为：

T(n)=∑i=1nlogi=1×0+2×1+...+2logn×logn=O(nlogn)\begin{aligned} T(n) &= \sum_{i=1}^{n}logi\\ &= 1\times0 + 2\times1 + ... + 2^{logn}\times{logn} \\ &=O(nlogn) \end{aligned}

通过把元素逐个入堆来建堆时，元素的时间复杂度可以用下图直观显示：

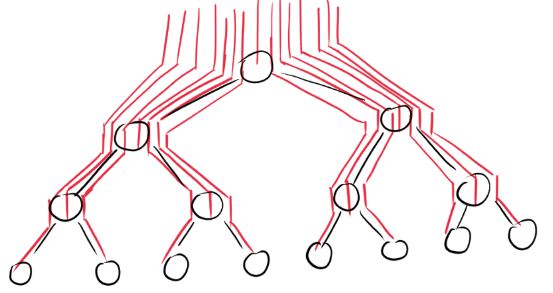
（每条红线的长度就是插入该元素所需的时间，红线的总长度就是建堆所需的总时间复杂度）

堆合并

我们就可以从树结构的最底层出发不断进行堆合并，小堆合并成大堆，最后合并到根节点就建成整个堆结构。

当节点的左右两个子树都是堆时，只需要对该节点进行下沉操作就可以合并左右两个堆。 不断进行堆合并，就是从下层开始把元素逐个下沉。

下沉第i个元素（从顶到底数）时，以其为顶点的树高度约为logn−logilogn-logi，则有下沉时间复杂度为：

T(i)=logn−logiT(i) = logn-logi

那么把所有元素下沉，则总时间复杂度为：

T(n)=∑i=1nlogn−logi=n2logn×logn+...+n4×2+n2×1=O(n)\begin{aligned} T(n) &= \sum_{i=1}^{n}logn-logi \\ &= \frac{n}{2^{logn}}\times{logn}+ ... + \frac{n}{4}\times2+\frac{n}{2}\times1 \\ &= O(n) \end{aligned}

同样的，我们也可以把逐个元素下沉所耗费的时间用下图来示意：

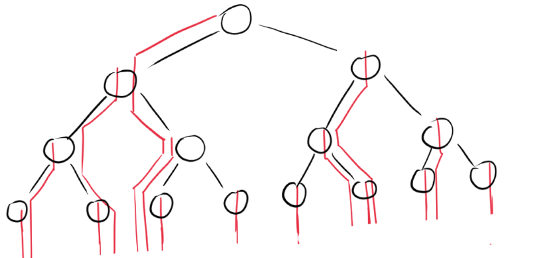
两种策略的比较与理解

逐个元素入堆的策略时间复杂度为O(logn)O(logn)，堆合并策略的时间复杂度为O(n)O(n)，为什么会出现差异呢？我们可以从两个角度来理解：

  1. 从元素移动路径的角度

    我们从前一小节的两幅图中可发现，元素入堆策略的图中根节点附近红线十分密集。而堆合并策略的红线则整体来说比较稀疏。

    这说明元素入堆策略中，在根节点附近元素做了较多重复无效的移动——也就是说插入一个元素时上浮到了根节点附近，然后又被其他后来的元素顶替下来。一上一下自然消耗了多余的时间，而这种消耗在元素入堆策略中出现频率高，无可忽视。

  2. 从元素移动数量与移动距离的角度

    我们知道一般来说树的越下层节点数量越多。特别是用数组实现的堆是个完全二叉树，最下层节点数量占了总数的一半。 因此建堆的时间复杂度主要取决于底层元素的移动距离。

    用元素入堆策略需要每个元素进行上浮操作，而偏偏元素数量最多的底层移动距离最长，O(n)O(n)个元素需要移动O(logn)O(logn)的距离，因此时间复杂度较高。

    而堆合并策略则反过来，需要每个元素进行下沉操作。移动距离最长的只有一个根元素，底层元素几乎不需要移动，因此时间复杂度加起来只有O(n)O(n)。

    如图所示，颜色越深代表移动距离越长。颜色深度对面积的积分即为建堆时间复杂度。

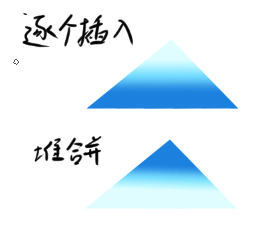
综上分析我们可以得出，通过堆合并策略建堆较优，时间复杂度只需O(n)O(n)。因此我们建堆一般采用堆合并策略，从下往上逐个元素下沉。

代码实现

其实理解了上面这些，要写一个堆出来也已经是水到渠成了。但正如Linus所说，Talk is cheap, show me the code。我们还是要亲手写一段，才能知道堆到底长啥样。

T = TypeVar("T")
class Heap(Generic[T]):
    '''堆结构
 
    有两个成员：
    self.A: List[T] # 堆内元素集合，元素类型为T，储存为数组
    self.fCompare: Callable[[T,T],bool] # 比较函数
    
    下面假设堆为大顶堆
    即有self.fCompare = lambda a,b: a>b
    '''

实现树结构

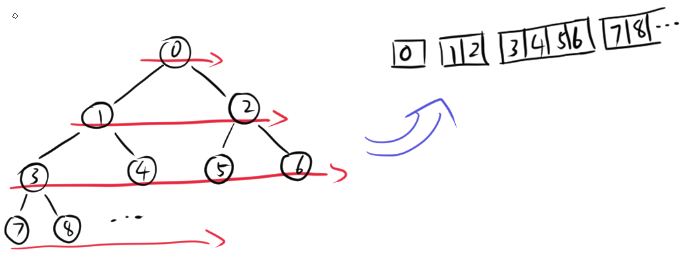
堆可以实现为基于数组的完全二叉树，以下标为零的节点为树根节点。

对于下标为i的节点，其左子节点、右子节点、父节点的下标分别如下所示：

def lfChildOf(i:int):
    return (i + 1) << 1 - 1
 
def rtChildOf(i:int):
    return (i + 1) << 1
 
def parentOf(i:int):
    return (i - 1) >> 1

至于为什么是这样，是因为完全二叉树与数组的对应规则如下图所示。这三个函数也没必要记住，到时候纸上画一画就记起来了。

实现基本操作——上浮与下沉

上浮

上浮就是递归地进行向上交换，下沉就是递归地进行向下交换。

def floatUp(self, i:int):
    '''上浮操作
 
    对下标为i的元素递归地进行上浮操作
    直到该元素小于其父节点或该元素上浮到根节点
    '''
    # 元素i上浮到根节点时结束递归
    if i <= 0:
        return
    
    # 当元素i小于其父节点时符合堆结构，结束递归
    pr = parentOf(i)
    if self.fCompare(self.A[pr], self.A[i]):
        return
    
    # 元素i大于其父节点，交换i与其父节点并继续上浮
    self.A[pr], self.A[i] = self.A[i], self.A[pr]
    self.floatUp(pr)

下沉

而下沉要稍微比上浮复杂。向下交换时，需要先找出较大的子节点，再跟较大的子节点进行交互。还要考虑左右子节点不存在的情况：当子节点下标超出堆大小时，子节点不存在。

def size(self):
    '''返回堆大小
    '''
    return len(self.A)
 
def sinkDown(self, i:int):
    '''下沉操作
 
    对下标为i的元素递归地进行下沉操作
    直到该元素大于其两个子节点或该元素下沉到叶子节点
    '''
    lc = lfChildOf(i)
    rc = rtChildOf(i)
 
    # 比较元素i与其两个子节点，获取三个元素中存在且最大的元素
    larger = i
    if lc < self.size() and self.fCompare(self.A[lc], self.A[larger]):
        larger = lc
    if rc < self.size() and self.fCompare(self.A[rc], self.A[larger]):
        larger = rc
    
    # 当元素i大于其两个子节点时符合堆结构，结束递归
    # 当元素i下沉到叶子节点时，左右子节点不存在，也会在此结束递归
    if larger == i:
        return
    
    # 元素i小于其中一个子节点，交换i与较大子节点并继续下沉
    self.A[larger], self.A[i] = self.A[i], self.A[larger]
    self.sinkDown(larger)

注意这里上浮和下沉操作使用了递归，会占用递归栈空间，因此额外空间复杂度并不是O(1)O(1)。

但上浮和下沉都可以改为循环迭代实现，迭代实现时额外空间复杂度为O(1)O(1)。要改成迭代实现并不困难，还请大家尝试自己实现。

实现各种借口——读、增、删、初始化

读取堆顶

堆一般只允许读取堆顶，即全堆最大元素。

def top(self):
    '''返回堆顶
    '''
    return self.A[0]

入堆

入堆时，把元素加到堆尾，再做上浮操作。

def insert(self, v:T):
    '''入堆
    '''
    # 将元素加到堆尾并做上浮操作
    self.A.append(v)
    self.floatUp(len(self.A) - 1)

出堆

出堆时，取出堆顶，把堆尾元素填到堆顶后，再做下沉操作。

def pop(self)->T:
    '''出堆
    '''
    # 取出堆顶元素
    res = self.A[0]
 
    # 将堆尾元素填到堆顶并做下沉操作
    self.A[0] = self.A[len(self.A) - 1]
    self.A.pop()
    self.sinkDown(0)
 
    return res

注意入堆与出堆操作都要保证堆的大小会相应变化。

堆初始化

堆的初始化采用堆合并策略，从堆尾到堆顶逐个元素做下沉操作。

def __init__(self, A:List[T]=[], 
             fCompare:Callable[[T,T],bool]=lambda a,b:a>b
             ) -> None:
    '''堆初始化
 
    :param A: 在数组A上进行初始化
    :param fCompare: 比较函数，对堆中节点p与子节点c，有fCompare(p,c)==True
    '''
    self.A = A
    self.fCompare = fCompare
    for i in reversed(range(len(A))):
        self.sinkDown(i)

整体代码

堆的整体实现

综上，堆的整体代码实现如下：

from typing import Any, Callable, Generic, List, TypeVar
 
T = TypeVar("T")
 
def lfChildOf(i:int):
    return (i + 1) << 1 - 1
 
def rtChildOf(i:int):
    return (i + 1) << 1
 
def parentOf(i:int):
    return (i - 1) >> 1
 
class Heap(Generic[T]):
    '''堆结构
 
    有两个成员：
    self.A: List[T] # 堆内元素集合，元素类型为T，储存为数组
    self.fCompare: Callable[[T,T],bool] # 比较函数
    
    下面假设堆为大顶堆
    即有self.fCompare = lambda a,b: a>b
    '''
    def __init__(self, A:List[T]=[], 
                 fCompare:Callable[[T,T],bool]=lambda a,b:a>b
                 ) -> None:
        '''堆初始化
 
        :param A: 在数组A上进行初始化
        :param fCompare: 比较函数，对堆中节点p与子节点c，有fCompare(p,c)==True
        '''
        self.A = A
        self.fCompare = fCompare
        for i in reversed(range(len(A))):
            self.sinkDown(i)
    
    def size(self):
        '''返回堆大小
        '''
        return len(self.A)
    
    def top(self):
        '''返回堆顶
        '''
        return self.A[0]
    
    def sinkDown(self, i:int):
        '''下沉操作
 
        对下标为i的元素递归地进行下沉操作
        直到该元素大于其两个子节点或该元素下沉到叶子节点
        '''
        lc = lfChildOf(i)
        rc = rtChildOf(i)
 
        # 比较元素i与其两个子节点，获取三个元素中存在且最大的元素
        larger = i
        if lc < self.size() and self.fCompare(self.A[lc], self.A[larger]):
            larger = lc
        if rc < self.size() and self.fCompare(self.A[rc], self.A[larger]):
            larger = rc
        
        # 当元素i大于其两个子节点时符合堆结构，结束递归
        # 当元素i下沉到叶子节点时，左右子节点不存在，也会在此结束递归
        if larger == i:
            return
        
        # 元素i小于其中一个子节点，交换i与较大子节点并继续下沉
        self.A[larger], self.A[i] = self.A[i], self.A[larger]
        self.sinkDown(larger)
 
    def floatUp(self, i:int):
        '''上浮操作
 
        对下标为i的元素递归地进行上浮操作
        直到该元素小于其父节点或该元素上浮到根节点
        '''
        # 元素i上浮到根节点时结束递归
        if i <= 0:
            return
        
        # 当元素i小于其父节点时符合堆结构，结束递归
        pr = parentOf(i)
        if self.fCompare(self.A[pr], self.A[i]):
            return
        
        # 元素i大于其父节点，交换i与其父节点并继续上浮
        self.A[pr], self.A[i] = self.A[i], self.A[pr]
        self.floatUp(pr)
    
    def insert(self, v:T):
        '''入堆
        '''
        # 将元素加到堆尾并做上浮操作
        self.A.append(v)
        self.floatUp(len(self.A) - 1)
 
    def pop(self)->T:
        '''出堆
        '''
        # 取出堆顶元素
        res = self.A[0]
 
        # 将堆尾元素填到堆顶并做下沉操作
        self.A[0] = self.A[len(self.A) - 1]
        self.A.pop()
        self.sinkDown(0)
 
        return res

单元测试

入堆、出堆等操作的简单单元测试如下：

import pytest
import heap
 
@pytest.fixture
def initHeap():
    return heap.Heap([1,3,4,7,2,6,5,9,0,8], 
                     lambda a,b:a>b)
 
class Test_TestHeap:
    def test_init_notNull(self, initHeap:heap.Heap):
        assert initHeap.size() == 10
        assert initHeap.top() == 9
    
    def test_insert_notTop(self, initHeap:heap.Heap):
        initHeap.insert(6)
        assert initHeap.size() == 11
        assert initHeap.top() == 9
    
    def test_insert_top(self, initHeap:heap.Heap):
        initHeap.insert(10)
        assert initHeap.size() == 11
        assert initHeap.top() == 10
    
    def test_pop(self, initHeap:heap.Heap):
        p = initHeap.pop()
        assert p == 9
        assert initHeap.size() == 9
        assert initHeap.top() == 8

关于堆排序

算法竞赛中除了原生使用堆结构以外，还有一个使用到堆的地方——堆排序。堆排序有原地排序、最坏时间复杂度为O(nlogn)O(nlogn)等优秀的性质，是比较常用的一个排序算法。

然而，手写堆排序要注意的地方与手写堆结构有比较大的不同。堆排序时要注意的点如下：

  1. 堆排序时一般要求在给入数组上原地排序，不需要内部维护一个数组结构，反之，需要记录堆结构的大小。
  2. 堆结构一般占用数组前端，因此从小到大排序时，有序部分从数组末尾开始扩张，建立的堆为大顶堆。
  3. 堆排序只需要建堆与出堆操作，因此只需要实现下沉操作。

关于堆排序的具体讨论，有机会的话我会另外写一篇来讲解。

数据结构
算法
算法竞赛
<- init-a-new-hexo-project
设计模式之美读书笔记 ->
Loading comments...